Queer Mathematical Joy:

Reflections from The “Camp” of Mathematical Queeries

(Part 1)

As many of you know, this summer I had the incredible opportunity to work with a small group of LGBTQ+ (entering) high school students for a mathematics enrichment program, “Camp” of Mathematical Queeries. The camp was probably the most joyful, affirming, and liberating experience I’ve ever had in mathematics. The majority of the students that registered, some entering 9th graders, some entering 10th graders, and some entering 11th graders, did not consider themselves as “math people,” but signed up because they were intrigued by the idea of a queer-centric mathematical space. One student, in her application to the camp, wrote “I’m only applying to this because my mom is making me.” LOL. While I was disheartened that this group of students had such a negative view of mathematics, I was also thrilled because this was the very group of kids that I was hoping would apply – those who had never seen themselves in mathematics or experienced any affinity for or joy in the subject. In this blog post I will discuss some of the learning that took place during the first half of “Camp,” in which we began developing a shared understanding about the non-neutrality of mathematics and the beauty and utility of mathematics, as well as developing our skills of mathematical problem posing. My plan is to follow up in the next two weeks or so with a second installment discussing the learning that took place during the second half of “Camp,” which is when we began exploring some of the mathematical questions we posed in the first few weeks. So, grab your cup of coffee and settle in, because here we goooooo…..

Week 1

We began our time together (we met 2 hours a day, MWF, for 5 weeks), with some basic community building activities, the first of which was to set community norms/agreements (see full activity here) that would carry us through the duration of the camp. As a group, students came up with the following three key agreements:

Be kind to ourselves and others
Be patient and supportive, especially when learning something new
Honor folx’s pronouns/names

I wanted to make sure we all had a shared understanding of each of these agreements, so I took our agreement-setting activity a step further and asked students to discuss, in breakout rooms, what it would look like, feel like, or sound like to keep to each of our identified agreements. Once students brainstormed ideas, they curated the following image to illustrate our community norms:

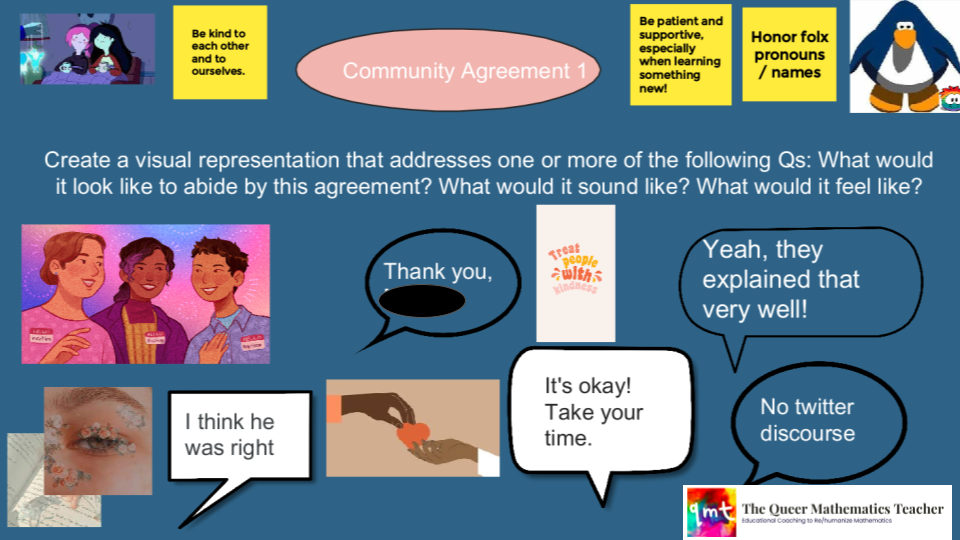
We came back to these agreements at the start of almost every session and reevaluated if 1) we were keeping to the agreements and 2) if we needed to change or add any new agreements. This led to a fourth agreement being added during week 2: Ask questions and share your thoughts!

The remainder of week 1 was spent on an icebreaker activity (of sorts) to introduce ourselves, and a discussion of the ways in which school (and mathematics classes specifically) work to reinforce heteronormativity. For our “get to know you” activity, I had students brainstorm a list of events, people, media, and/or ideas that have shaped their queer identity and a list of events, people, media, and/or ideas that have shaped their feelings about math (see full activity directions here). After the brainstorming session, I asked students to select at least six of their brainstormed items (preferably three for queer identity and three for math) and to find some song, image, poem, quote, or other artifact(s) that represented those items. The goal was to make a collage with these items, to be shared with the group during our next session.

For reference, I shared the following slide with students, which contained two items from my own brainstorm. On the left is a picture of Sandra Bauser’s Pushing Boundaries. Along with a quotation from Ocean Vuong. I explained to students that the image and quote both represented the significant impact my queer identity (which is ever evolving) has had and continues to have on my beliefs about mathematics and the teaching and learning of mathematics. The image on the left is a Mark Wang illustration for the NYT article “How to Disclose a Disability to Your Employer (and Whether You Should)” and is accompanied by an Edith Windsor quote. I explained that these were a representation of my almost two year recovery from a mild traumatic brain injury. While the recovery was brutal and in many ways filled with despair, it also provided an opportunity for me to engage in a self-exploration of my queer identity and the ways in which heteronormativity was leading me to hide parts of myself. This eventually led me to a commitment to live more authentically, to pursue opportunities, work, and relationships that brought me joy and to let go of those that did not.

I asked students to turn their cameras off as we worked throughout the remainder of the session and listened to a playlist I had curated, based on a survey they filled out prior to the camp (which asked them to identify a few songs that were “giving them life”). When we reconvened on Friday of the first week, we spent about half of the session finishing up and sharing our collages. For the final half of the sessions I asked the students to consider the ways in which schools and mathematics classrooms reinforced heteronormativity (first we all discussed what the term heteronormativity meant to us). Their thoughts are captured in the image below.

One student (who is nonbinary) described how their teachers often group students in collaborative groups of “all” boys or “all” girls, leaving no space for them as a nonbinary person. They also laughed and said, “one teacher told me the reason they split by gender was because they didn’t want boyfriends and girlfriends to end up in the same group…little did they know they had put me in an “all-girl” group with my girlfriend, so I guess it worked to my advantage?” Another student referenced the “they were just good friends” troupe that is often repeated in classrooms when discussing stories or historical accounts in which there are obviously queer understones. As an example, she noted a recent class in which the teacher had assigned students to read The Iliad. While Homer does not explicitly state Patroclus and Achilles are lovers, queer undertones are present throughout their relationship in the story. The student discussed how the teacher’s lack of acknowledgement or ability to discuss those queer undertones was frustrating and helped to reinforce the idea that the things you learn at school are just that, nothing more. “School learning” does not reflect the actual complexity of everyday life and is thus, incredibly boring and irrelevant.

This discussion led naturally into one of mathematics and the ways in which students are often asked to solve unrealistic problems like the one shown in the meme below.

Click here for image source

In relation to their queer identities, students also noted that they had never seen their queer identities reflected in mathematics problems. They felt frustrated that math problems asking about “couples” always invoke a heteronormative conception of a couple and those involving gender are limited to the gender binary. We discussed how this impacts how welcome we feel in mathematical contexts and how it often leads us think twice (or thrice!) about everything, ranging from our body language in class to our willingness to engage in creative/inventive ways of thinking about and doing mathematics.

The students’ examples and discussion of heteronormativity resonated deeply with me as a queer mathematics educator. It reminded me of the ways in which queer bodies and expression is policed in both overt and subtle ways throughout our K-12 schooling (see Harper Keenan’s “Unscripting Curriculum“). Mathematics classrooms are not exempt from this. In fact, I would argue that mathematics classrooms are some of the most violent spaces for queer students, given the many ways normativity (not just heteronormativity) is valued and reinforced in K-12 mathematics classrooms (e.g., normative ideas such as finding the “acceptable” answer by using the “acceptable” solution method). This is likely why we see fewer LGBTQ+ folx pursuing STEM careers (or even making it to higher level math in HS, as noted in this blog post by Dr. Kyle Whipple) than their non-LGBTQ+ peers. I’d also say it’s likely why we see so many queer folx drawn to the arts and humanities, where there is a perception of more nuance in what counts as knowledge and who counts as a creator of knowledge.

Week 2

During our second week of “Camp” our opening discussions centered on four questions

Is math invented or discovered?
Why do so many people hate math?
Is math useful?
Is math neutral?

I prefaced each of these questions by playing one (or more in the case of Qs 3 and 4) TikTok video(s) by mathematics communicator and drag queen, Kyne Santos. This page contains the videos we viewed to frame our discussions of each of the questions.

Side Note: if you are not following Kyne on social media (TikTok, Insta, Twitter, or YouTube) I suggest you check out her TikTok (or one of her other social media accounts) immediately after you finish this blog post!

These videos and questions led to rich conversations about students’ implicit beliefs about mathematics and the biases and systemic oppression that are reinforced through mathematics. For the video in relation to “Is math invented or discovered,” Kyne states she believes mathematics is discovered because it was developed independently by various cultures and is present throughout the world and universe. She states that while we might come up with the language to describe mathematics as a means to understand the world around us, we did not invent it. She says, “nobody sat down and said hmmmm the three angles of a triangle should add up to 180 degrees because I like that number.” This led to a lively debate in which some students agreed with Kyne and others argued that since mathematics is a social construct, it is, in fact, invented. They stated that by “coming up with the language of mathematics” humans are engaging in an act of invention. While there was no consensus on these ideas, the discussion was intriguing and complex and showed me that students were deeply engaged with the question and understanding each others’ beliefs about mathematics.

Our discussions of the videos and ideas in relation to questions 2-4 were just as lively as the first. Students made connections between the three videos stating that because school mathematics is often perceived as useless (see watermelon problem and discussion about not reflecting reality above) and is perceived as neutral, many people develop a deep disliking of the subject. They also noted that because people dislike the subject and have so many beliefs about its neutrality and superiority in society, we are now entering an age of misinformation and a deep distrust of “experts.” They said this was because of the misuse of mathematics to help perpetuate systemic oppression and other claims that are misleading and grounded in inappropriate assumptions and interpretations (see the page of Kyne videos linked above for examples). Like Kyne stated in her “Why do so many people hate math?” video, the students believed that if mathematics was presented as non-neutral, useful, and in interesting contexts like those Kyne highlights in her videos, then mathematics would be viewed in a very different light and would be seen as a tool of empowerment, to be used to understand the world and enact systemic change. What a liberating mathematics that would be! After completing our discussion of the four questions, and much to the students surprise, we had a special guest drop in — Kyne Santos herself!

Side note 1: Not gonna lie, I probably fangirled way more than them, but whatevs.

Side note 2: Thanks so much Kyne for taking the time to join us! The students really enjoyed it!

While she was with us, Kyne introduced students to a number of engaging problems from higher level mathematics and discussed how problems like these are what drew her to the field. Check out a few of Kyne’s slides below!

Taking too long?

Reload document

Open in new tab

Kyne’s visit was impactful for a number of reasons. First, her presence (and mere existence) was an affirming experience for the students, many of whom had never seen themselves or people like them in mathematics. The presence of a drag queen that makes a living doing mathematics and does so in cool and meaningful ways was….well, mind blowing and possibly even life changing. Second, Kyne both introduced and broke down higher level mathematics in a way that was engaging and accessible, showing students that understanding higher level mathematics is not only possible, but can be fun! Third, Kyne’s visit helped to move us into a discussion about what counts as mathematics (e.g., the idea that the reddit debate surrounding the question “how many holes are in a straw” was an application of topology was eye opening to students) and the idea that anyone can pose a mathematical question. This was a great segue into our next set of activities, mathematical problem posing.

Throughout the remainder of week 2 (and start of week 3), we focused our energy on methods of problem posing. To preface our discussion, I first had students watch the below video from Arup, which presents the concept of queering public space.

I sent students into breakout rooms to discuss the question “given the discussion in the video, how would you envision a queer space?” Following this, using a model I adapted from a workshop given by my dear friend Arundhati Velamur (who actually joined us for this session!), I engaged students in the start of a mathematical problem posing exercise using the following four slides.

Taking too long?

Reload document

Open in new tab

As expected, students initial response to the image was to record noticings, rather than wonderings. Their initial observations are shown in the image below.

Next, I had students read (independently), then discuss an article in which the artist of the piece discussed their design and intentions. Students used the context provided in the article, as well as the following questions to help craft their initial noticings into wonderings.

Is there something about space and shape that might be interesting regarding these images?
Is there a symmetry to be considered?
What purpose do the objects in the images serve? How might those purposes help our questioning?
Is there something about the way the items in the images were constructed that might be interesting? How might those inform our questioning?

Before we sent students off to do this, Arundhati and I created what we called a “scratch pad” for each student. The scratch pad was a google drawing document, which allowed each student to draw shapes, scribble, and type questions directly on the Boudoir Babylon image. Arundhati and I also demonstrated how we used the scratch pad and the posed questions to come up with a few of our own sample wonderings (see image below).

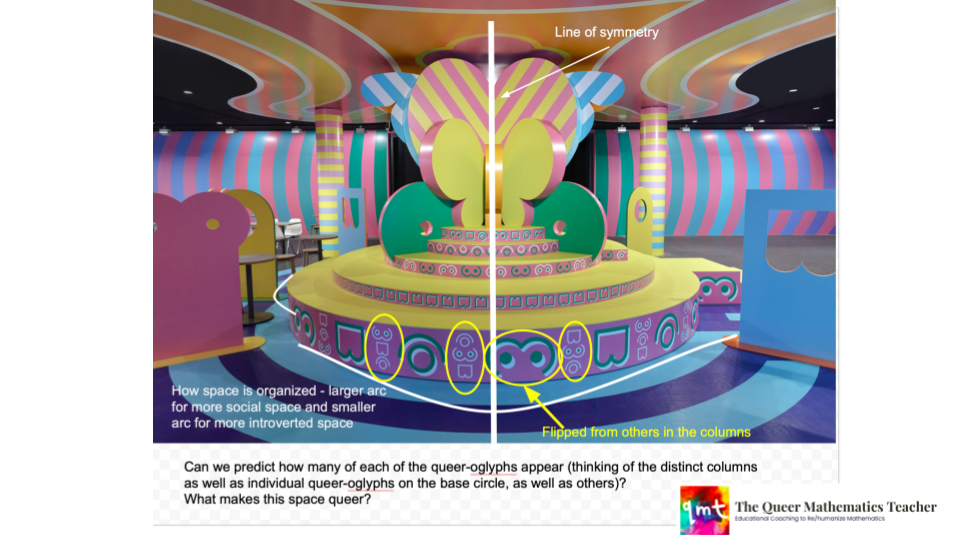
After working for a few minutes independently on their scratch pads, we gave students time to discuss their questions and further refine them in breakout rooms before we came back together. This resulted in the final list of noticings/wonderings shown below.

Students repeated this process for posing mathematical questions for a number of other images and graphs that we observed in the following sessions (some of which will be discussed in a future blog post). After each instance of problem posing, we filed away our posed questions and made note of those that we found most interesting and/or thought we might be able to solve. We would return to these questions in the final weeks of “Camp” and engage in various mathematical activities designed to work toward an answer or better understanding. For more on that….stay tuned!

If you’re interested in delving more deeply into the mathematics and pedagogical methods described in this blog post, I encourage you to sign up for my 6-part professional development series: Visions of a Re/humanized Mathematics for LGBTQ+ Students (see image below). The series is designed for mathematics teachers and coaches/teacher educators of pre- and in-service math teachers in grades 6-12. Over the course of 6 sessions, we will delve more deeply into the relationship between queer and mathematical identity and queer theory/ pedagogy. Participants will have the opportunity to engage in some of the mathematical activities that I designed based on the questions students’ posed during “Camp,” as well as other mathematics examples of queer pedagogy designed for (and in many cases implemented with) middle and high school students. Towards the end of the series, I will provide time for and guide participants in creating their own example of a task or lesson that utilizes queer theory and to receive feedback from both myself and their peers. The goal is to leave the series with a (small) bank of preliminary tasks and lesson plans that are LGBTQ+ inclusive and affirming. For more information visit www.TheQueerMathematicsTeacher.com/Visions.

En comunidad,

Queer Mathematical Joy:

Reflections from The “Camp” of Mathematical Queeries

(Part 1)

Week 1

Week 2

Receive awesome QMT-created content in your inbox.